Субота, 12.07.2025, 11:58Вітаю Вас Гість | RSS
Зовнішнє оцінювання
Головне меню
Календар
«  Липень 2025  »
ПнВтСрЧтПтСбНд
 123456
78910111213
14151617181920
21222324252627
28293031

Главная страница

Вектор
<br /> Геометричний вектор — у фізиці і математиці це величина, яка характеризується числовим значенням і напрямком. В фізиці є чимало важливих величин, які є векторами, наприклад сила, положення, швидкість, прискорення, кутовий момент, імпульс, напруженість електричного і магнітного полів. Їх можна протиставити іншим величинам, таким, як маса, об’єм, тиск, температура та густина, які можна описати звичайним числом, їх називають «скалярами». <p> Графічно вектори зображають у вигляді напрямлених відрізків певної довжини . Наприклад, для графічного представлення сили величиною два Ньютони, треба намалювати відрізок прямої довжиною дві одиниці в напрямку дії сили. Стрілка вказує, що сила діє від точки A до точки B; якби сила діяла від B до A, то треба було б записати . Чисельне значення вектора А називається модулем чи довжиною і позначається |A|. Ця величина - скаляр. Два паралельних вектори, що мают <!-- ... Читати далі »
Переглядів: 3057 | Додав: regikso | Дата: 14.06.2010 | Коментарі (3)

Перетворення подібності
<br /> Перетворення подібностi <p> Перетворення фігури F у фігуру F ' називається перетворенням подібності, якщо при цьому перетворенні відстань між точками змінюється в одну й ту саму кількість разів (мал. 1). Це означає, що коли довільні точки X та Y фігури F при перетворенні подібності переходять у точки X' і Y' фігури F', то X'Y'=k .XY, причому число k – дне і те саме для всіх точок X і Y. Число k називається коефіцієнтом подібності. Якщо k=1, перетворення подібності, очевидно, є рухом. <br /> Нехай F – дана фігура і O – фіксована точка (мал. 2). Через довільну точку X фігури F проведемо промінь OX і відкладемо на ньому відрізок OX', що дорівнює k,де k – додатне число. Перетворення фігури F, при якому кожна її точка X переходить у точку X', побудовану таким способом, називається гомотетією відносно центра O. Число k називається коефіцієнтом гомотетії, фігури F і F' називаються гомот <!-- ... Читати далі »
Переглядів: 2085 | Додав: Artyk | Дата: 07.06.2010 | Коментарі (0)

Парлельний перенос
Параллельный перенос <br /> Параллельный перенос ― частный случай движения, при котором все точки пространства перемещаются в одном и том же направлении на одно и то же расстояние. Иначе, если M ― первоначальное, а M' ― смещенное положение точки, то вектор ― один и тот же для всех пар точек, соответствующих друг другу в данном преобразовании. <br /> <p> Параллельный перенос перемещает каждую точку фигуры или пространства на одно и то же расстояние в одном и том же направлении. <br /> На плоскости параллельный перенос выражается аналитически в прямоугольной системе координат при помощи <br /> <br /> где вектор . <br /> Совокупность всех параллельных переносов образует группу, которая в евклидовом пространстве является нормальной подгруппой группы движений, а в аффинном ― нормальной подгруппой группы аффинных преобразований.
Переглядів: 1291 | Додав: Artyk | Дата: 07.06.2010 | Коментарі (0)

Осьова симетрія
Осьова симетріяВідбиття фігури F в осьовій симетрії S відносно прямої p: F1 = Sp(F) <br /> Осьова симетрія, симетрія відносно осі — в евклідовій геометрії — вид дзеркального відбиття, при якому множиною нерухомих точок є пряма, яку називають віссю симетрії. <br /> Для фігури, що переходить сама в себе при осьовій симетрії, пряма, утворена нерухомими точками руху, називається віссю симетрії фігури. Прикладом осі симетрії відрізка є його серединний перпендикуляр. <br /> Будь-який рух площини можна представити у вигляді композиції не більш ніж трьох осьових симетрій. <br /> Осьова симетрія у кристалічному тілі <br /> Апарат теорії симетрії є основою мови, що описує геометрію кристалічних многогранників та кристалічних решіток. У кристалічному тілі існують: <br /> • Прості поворотні осі 1-, 2-, 3-, 4- та шостого порядків (С1, С2, С3, С4, С6). Завдяки внутрішній будові (дальній порядок) за принципом <!-- ... Читати далі »
Переглядів: 3142 | Додав: Artyk | Дата: 07.06.2010 | Коментарі (0)

Поворот
Поворот <p> Поворот (обертання) - рух, при якому принаймні одна точка площини (простори) залишається нерухомою. <p> У фізиці нерідко поворотом називається неповне обертання, або, навпаки, обертання розглядається як приватний вид повороту. Останнє визначення строгіше, оскільки поняття поворот охоплює значно ширшу категорію рухів, у тому числі і таке, при якому траєкторія рухомого тіла в обраній системі відліку є незамкнутою кривою. <p> * <p> Пов'язані визначення <p> * нерухома точка називається центром обертання, нерухома пряма називається віссю обертання і т. д. <p> Типи обертань <p> * Обертання площини (простори) називається власним (обертання першого роду) або невласним (обертання другого роду) залежно від того, зберігає воно або немає орієнтацію площини (простори). <br /> o Невласне обертання не можна зробити малим (у сенсі відстані між кожною точкою і її чином), власне - можна зробити скільки завгодно <!-- ... Читати далі »
Переглядів: 1162 | Додав: Artyk | Дата: 07.06.2010 | Коментарі (0)

Центральна симетрія
Центральна симетрія <br /> Центру́льной симме́три́їй відносно точки A називають перетворення простору, що переводить точку X в таку точку X′, що A - середина відрізку XX′. Центральна симетрія з центром в точці A зазвичай позначається через ZA, тоді як позначення SA можна переплутати з осьовою симетрією. Фігура називається симетричною відносно точки A, якщо для кожної точки фігури симетрична нею точка відносно точки A також належить цій фігурі. Точка A називається центром симетрії фігури. Говорять також, що фігура має центральну симетрію. <p> Інші назви цього перетворення - симетрія з центром A. Проте можна помітити, що центральна симетрія є часткою випадком повороту, а саме, повороту на 180 градусів <br /> • <br /> Пов'язані визначення <br /> • Якщо фігура переходить в себе при симетрії відносно точки A, то A називають центром симетрії цієї фігури. <br /> Загальні властивості <br /> • <!-- ... Читати далі »
Переглядів: 2422 | Додав: Artyk | Дата: 07.06.2010 | Коментарі (0)

Методи геометричних перетворень
Вказанi види дiяльностi недостатньо поданi i у змiстi навчання, і у сучасних засобах навчання, i на всiх ступенях навчання геометрії. Обгрунтування цього висновку потребує додаткових аргументiв. Однак достатньо лише звернути увагу на те, що в наявних засобах навчання геометрії дуже мало завдань на роботу з рисунком, щоб переконатись у цьому. Конструювання образiв практично обмежується побудовою рисункiв до задач. Цього занадто мало. <p> Увага до переміщення образiв цілком характеризує подання геометричних перетворень у сучасних вiтчизняних засобах навчання. Ще менше уваги в засобах навчання геометрiї придiляється найважливiшим видам дiяльностi, якi характеризують сформованість образного мислення, — перетворенню образiв і їхнiй побудовi. <p> Яскравою ілюстрацiєю недостатньої спрямованостi змiсту навчання геометрiї у школi на формування просторового мислення є культивацiя <!-- ... Читати далі »
Переглядів: 1578 | Додав: Artyk | Дата: 07.06.2010 | Коментарі (0)

Векторний метод
Векторне розв'язування геометричних задач може проводитися і без введення системи координат. У цьому випадку звичайно вибирають на площині два неколінеарні вектори, а в просторі – три некомпланарні (не паралельні одній площині) вектори як основні (їх звичайно називають базисні вектори) і виражають решту векторів через базисні. Для зручності запису базисні вектори позначають малими буквами латинського алфавіту – тощо. <br /> Задача 33. У паралелограмі АBСD (Рис.48) АВ=2ВС і М – середина сторони СD. Довести, що відрізки АМ і ВМ перпендикулярні. <br /> Розв'язання. Щоб довести, що відрізки АМ i BM перпендикулярні, досить довести, що скалярний добуток векторів i дорівнює нулю. <br /> Виберемо базисні вектори (найчастіше їх вибирають так, щоб вони виходили з однієї точки): і . <br /> Виразимо потрібні нам вектори i через базисні. Оскільки М – середина DС, то і . <br /> Знайдемо скалярний добуток в <!-- ... Читати далі »
Переглядів: 1240 | Додав: Artyk | Дата: 07.06.2010 | Коментарі (0)

Приклади з модулем
<p> Приклади з модулем <p> Модуль трапляється в конкурсних завданнях при розв’язуванні різних прикладів, причому досить часто, тому потрібно чітко усвідомлювати його означення. Формально модуль означається за допомогою формули . Тут головним є те, що для розв’язування прикладу треба позбутися вертикальних рисочок. <p> Нагадаємо схеми розв’язання деяких основних типів рівнянь з модулем: <p> 1.) <p> 2.) <p> 3.) <p> Приклад. Розв’язати рівняння . <p> Якщо абсолютні величини рівні, то числа рівні або протилежні: <p> Відповідь: . <p> Приклад. Розв’язати рівняння . <p> Оскільки рівність задає на числовій прямій геометричну множину точок, сума відстаней від яких до двох заданих точок з координатами –2 і 6 дорівнює 8, то відповідно буде – безліч розв’язків. <p> -2 6 х <br /> <p> Відповідь: . <p> Таким чином, можемо зробити наступне зауваження: <p> Зауваження. Деякі рівняння (нерівності) з абсолютн <!-- ... Читати далі »
Переглядів: 3323 | Додав: regikso | Дата: 07.06.2010 | Коментарі (0)

Координатний метод
Метод координат – це один із найбільш універсальних методів геометрії. В принципі майже будь-яку геометричну задачу можна розв'язати методом координат. Проте спроби розв'язувати кожну задачу лише координатним методом (маються на увазі, звичайно, ті задачі, в умові яких не говориться про координати) часто призводять до того, що навіть проста геометрична задача стає дуже складною алгебраїчною. <br /> Головне при розв'язуванні геометричних задач координатним методом – вдалий вибір системи координат, тобто вибір початку координат і напряму осей. Звичайно за осі координат вибирають прямі, що фігурують в умові задачі, або осі симетрії (якщо вони є) фігур, розглядуваних у задачі. Бажано, щоб вибрана система координат природно визначалася умовою задачі.
Переглядів: 2080 | Додав: Artyk | Дата: 07.06.2010 | Коментарі (0)

1 2 3 »




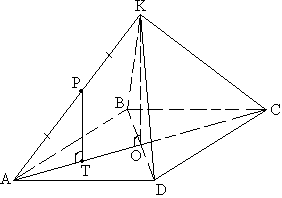
Бічне ребро правильної чотирикутної піраміди з основою складає кут а. А середина цього ребра віддалена від основи на відстань m. Знайти об'єм піраміди.
рисунок к задаче 82 №1
1.
а).
Оскільки піраміда правильна, то кути КАВ і КАd рівні. Основа АВСd - квадрат. Кут КАО є а
Теорема. Нехай дані три пересічні прямі, не лежачі в одній площині. Опустимо перпендикуляр з вільного кінця однієї з прямих на площину, утворену двома іншими прямими. Цей перпендикуляр впаде на бісектрису кута, утвореного двома іншими прямими тоді і лише тоді, коли дана пряма утворює з двома іншими прямими рівні кути.
Теорема. Діагоналі ромба (у окремому випадку квадрата) є біссектриссами його кутів і перетинаються під прямим кутом.
Виходячи з цих теорем, визначаємо, що перпендикуляр РТ падає на АС.
би).
Прямокутні трикутники АКО і АРТ подібні по гострому куту КАО, причому АК = 2АР за даними. Значить:
АТ = 2АТ і До = 2РТ = 2m
у).
З прямокутного трикутника АРТ:
АТ = РТctgа значить
АТ = 2АТ = 2mctgа
АС = 2АО = 4mctgа
Знайдемо площу основи- квадрата по наявній діагоналі:
S = AC2/2 = 8m2ctg2а

2.
а).
По наявній висоті До і площі підстави S знайдемо об'єм піраміди:
нахождение объема
Архів записів
Друзі сайту
Block title